
Is it possible for a theoretical species to have exactly 3, equally represented phenotypes?
May 7, 2018

- Related Topics:
- Quirky questions,
- Dominant and recessive,
- Editor's choice,
- Population genetics,
- Evolution
A high school student from Texas asks:
"Is it possible for there to be three phenotypes (and only three) that are equally represented in a species? (Such as for blood types, except A, AB, and O are all equally represented.) Theoretically, what would have to be the conditions to allow for equal representation of three different phenotypes?
This is for creative writing, so feel free to take any liberties in assuming the theoretical world’s other aspects!"
This is a great question! Yes, it could be possible for your theoretical species to have three equally represented phenotypes. And you can prove it with math.
Before I get to the answer, I should begin with a few definitions:
-
A phenotype is your version of a trait. Like curly vs straight hair.
-
An allele is the term geneticists use to refer to a version of a gene. For example, a hair texture gene might come in two versions: curly or straight
-
A genotype is your combination of genes. Perhaps you have two straight hair alleles.
Now that we have a grasp on those, let’s get into the answer!
Could incomplete dominance be a solution?
There are many ways to have exactly three phenotypes for a trait. Perhaps the simplest way is incomplete dominance.
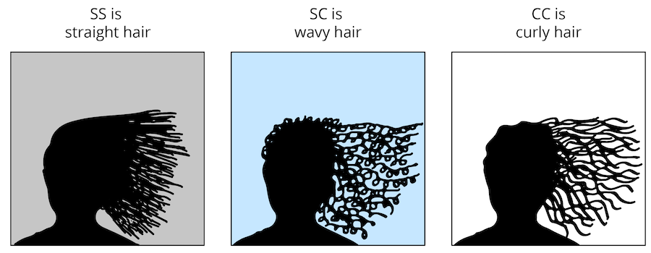
Straight vs curly hair is one classic example of this. Let’s pretend for a moment there are two versions of a gene for hair texture: straight and curly. And remember, you have two copies of each gene, one inherited from each parent.
That gives you three possible combinations of this gene, which give the following hair textures:
Straight + Straight = straight hair
Curly + Curly = curly hair
Straight + Curly = wavy hair
That last combination is what makes this an example of incomplete dominance. In a classic dominant vs recessive gene, you would expect one of the two versions to be stronger. That’s not the case here, where both versions are equally strong. If you have two different versions of this gene, you get a phenotype that’s somewhere in between.
However, you asked for something a little different. You wanted three phenotypes that are all equally represented in the population. Can we get an equal number of people with straight, curly, and wavy hair?
It turns out this isn't possible with incomplete dominance. Let’s walk through how you can prove this, before getting into a more complex example that could give you a solution.
Testing the hypothesis with Hardy-Weinberg
For a moment, let’s continue to pretend that there’s only one gene for hair texture, and it comes in two versions: straight and curly. We can call the straight hair allele “S” and the curly hair allele “C.”
Everyone has two copies of the hair texture gene. Their genotype will determine what kind of hair they have.
Geneticists like to use the model of Hardy-Weinberg equilibrium when we look at traits in a population. This model uses a few assumptions which let us convert between allele frequency and phenotype frequency.
If we know the rate of the straight hair and curly hair alleles, we can then predict how many people will have straight, curly, or wavy hair.
When we talk about two alleles, we call the frequencies of those alleles “p” and “q”. So for hair texture, p is the frequency of the straight hair allele, and q is the frequency of the curly hair allele. Since they are the only two alleles, we know that they must add up to 100% (or, 1).
This gives us the following formula:
Equation 1: p + q = 1
Next, we can square each side of this equation. Remember that the two sides of the equation are still equal if we do the same thing to both of them!
(p + q)2 = 12
Well, 12 = 1, so we get:
(p + q)2 = 1
Let’s finish by expanding the left side:
Equation 2: p2 + 2pq + q2 = 1
Now, what do each of those parts mean?
Well, “p2” means “the frequency of the straight hair allele times the frequency of the straight hair allele”. In other words, it means how often someone will have the straight hair genotype (SS).
Similarly, q2 is the frequency of the curly hair genotype (CC).
The frequency of the wavy hair genotype (SC) is 2pq. The ‘2’ in that part is because there are two ways of getting the wavy genotype. The first way is to get the straight allele from dad and the curly allele from mom. The second way is to get the straight allele from mom and the curly allele from dad.
In other words:
p2 is people with straight hair (SS)
2pq is people with wavy hair (SC)
q2 is people with curly hair (CC)

Incomplete dominance can't lead to equal phenotypes
So now that we know the formulas of Hardy-Weinberg equilibrium, is there a way for these three phenotypes to be equally represented? The answer is no!
Let's walk through the Hardy-Weinberg equations to see why not.
Let’s choose to start with straight hair. We just learned that the frequency of the straight hair genotype is p2. If people with straight hair are a third of the population, then:
p2 = 1/3
When we solve that equation, we get p = 0.577. So far, no problem. Now we need to figure out q, which we can do with Equation 1:
p + q = 1.
Substituting in the value we found for p, we get:
0.577 + q = 1
q = 0.423
Using these values for q and p gives us 2pq = 0.488 and q2 = 0.179.
That means you would end up with this set of frequencies:
Straight hair = 33%
Wavy hair = 49%
Curly hair = 18%
It also does not matter which phenotype we solve for first. No matter how we slice up the values of p and q, we cannot get to 33% for each phenotype under Hardy-Weinberg equilibrium.
I mentioned that Hardy-Weinberg equilibrium uses a few assumptions. These are actually quite big assumptions. If we use more complex models which don’t have those assumptions, we can get closer to equal representation of our three phenotypes. However, the math gets pretty tricky. Let’s see if there’s still a way to find a simple solution.
Three’s Company: A dominance series
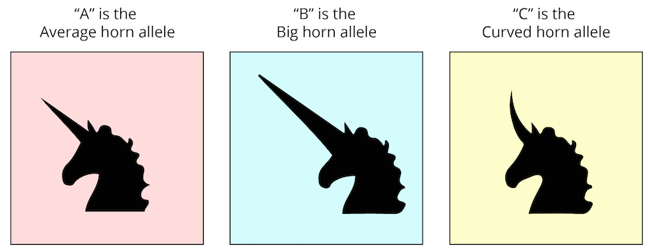
It turns out we can get our solution by adding one more allele into the mix! Let’s make up an example here. Unicorn horn shape is a three-allele system:
We want to stick to three phenotypes here. Usually, more versions of a gene means more possible phenotypes. However, three alleles can produce exactly three phenotypes when those alleles are in a dominance series.
In a dominance series, version A of the gene is dominant to version B, which is in turn dominant to version C. We can represent this as A > B > C.
For our unicorns, average horns are dominant to big horns. Big horns are dominant to curved horns. Finally, curved horns are recessive, completing our dominance series: A > B > C.
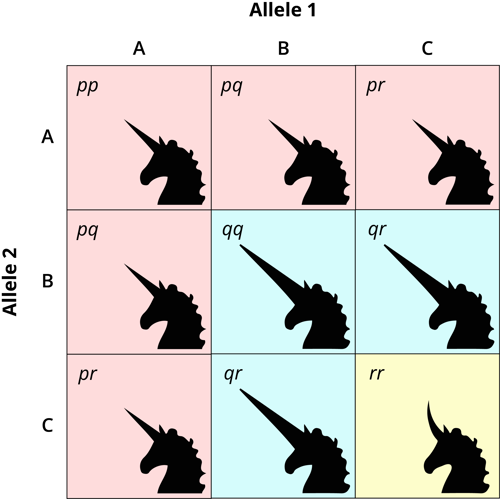
When we have three alleles, we have six possible genotypes. For our unicorns, they are as follows:
AA = average horns
AB = average horns
AC = average horns
BB = big horns
BC = big horns
CC = curved horns
Notice that even though we have six genotypes, we still have only three phenotypes.
Now let’s look at Hardy-Weinberg equilibrium with our horn alleles. Let’s call the frequency of the average horn allele “p”. The frequency of the big horn allele can be “q,” and the frequency of the curved horn allele will be “r.” Allele frequencies still must add up to 100%, giving us
Equation 3: p + q + r = 1
This is just like Equation 1 up above, but with an extra allele. Like we did before, we are going to square both sides of this equation, resulting in
Equation 4: p2 + 2pq + 2pr + q2 + 2qr + r2 = 1
As with Equation 2, each term here represents the frequency of one of the genotypes. Together, they must add up to 100%. This time, multiple genotypes match to each of our phenotypes.
p2 + 2pq + 2pr is unicorns with average horns (AA, AB, and AC)
q2 + 2qr is unicorns with big horns (BB and BC)
r2 is unicorns with curved horns (CC)
Now, let’s see if we can figure out how to get each horn phenotype equally represented.
First, let’s solve for the frequency of the curved horn allele. If a third of the unicorns have curved horns, then
r2 = 1/3
This looks familiar. The frequency of the curved horn allele is r = 0.577.
Next, let’s solve for the frequency of the big horn allele. We also want a third of the unicorns to have big horns. Looking at the results of equation 4 above, we know the frequency of the big horn phenotype is q2 + 2qr, so
q2 + 2qr = 1/3
Since we already know that r = 0.577, we can substitute that into our equation:
q2 + 1.154q = 1/3
From here, we can use the quadratic formula to solve for q. The frequency of the big horn allele is q = 0.239.
Finally, we can put the values we found for q and r into Equation 3 to solve for the frequency of the average horn allele.
p + q + r = 1
p + 0.239 + 0.577 = 1
p = 0.184.
Just to double check our result, let’s solve for the frequency of the average horn phenotype, which is:
p2 + 2pq + 2pr
Putting in the values we found for each allele, we get:
p2 + 2pq + 2pr =
0.1842 + (2 * 0.184 * 0.239) + (2 * 0.184 * 0.577)
= 0.334
Therefore, the frequency of our average horn phenotype is also 1/3 (with a little rounding error). So there you have it! We have found a way to get three phenotypes in equal proportion in a population.
Average horns = 33%
Big horns = 33%
Curved horns = 33%
In this solution, we used a three-allele dominance series. If our series is A > B > C, then the frequencies of the A, B, and C alleles are 18%, 24%, and 58%.

Author: Robert Coukos
When this answer was published in 2018, Robert was a Ph.D. candidate in the Department of Genetics, studying protein engineering and directed evolution in Alice Ting's laboratory. He wrote this answer while participating in the Stanford at The Tech program.
 Skip Navigation
Skip Navigation
